Today’s post is based on the master thesis of Arturo Barrabés Castillo titled Design of Single Precision Float Adder (32-bit Numbers) according to IEEE 754 Standard Using VHDL.

Since DLS doesn’t support more than 16 bits per wire/pin, I’ll apply the same algorithms on 16-bit floating point numbers. I kept the same component names to easily find the connection between the paper and the schematics below. There are also some differences from the paper which I’ll point out when describing the relevant part of the circuit.

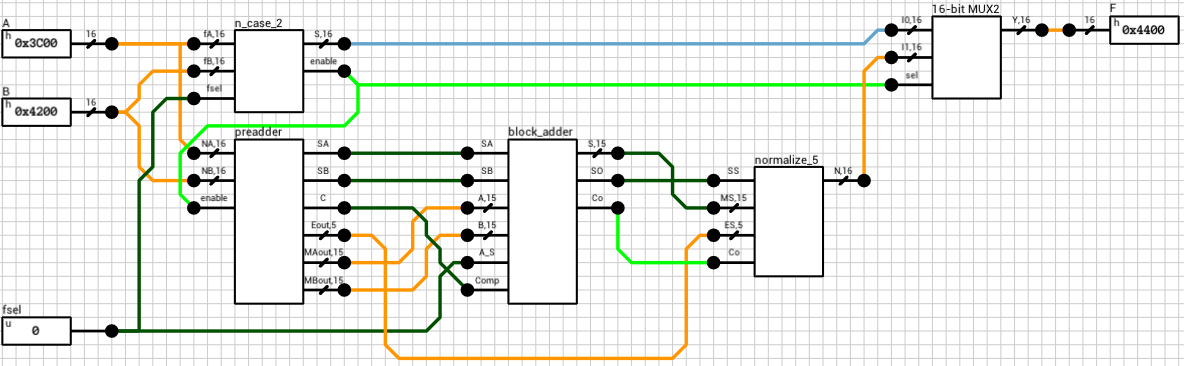
Figure 1 shows the final component. It has 3 inputs (A, B, and fsel) and 1 output (F). A and B are the two 16-bit floating point numbers. fsel is the function select signal, with 0 for addition and 1 for subtraction. F is the result of the operation.

Step 1: Check for a special case

The first step is to check if we have a special case. Special cases are considered all the cases for which the result of the operation between the 2 inputs can be determined without performing the operation. I.e. adding 0 to a number results in the number itself, adding opposite sign infinities results in a NaN, etc. (see the paper for all the cases).

The block handling this part is called n_case (figure 2). It has 2 outputs, S and enable. S is the result of the operation if a special case is detected, otherwise Undefined. enable is used to turn on the rest of the circuit in case the current combination cannot be handled by this block.

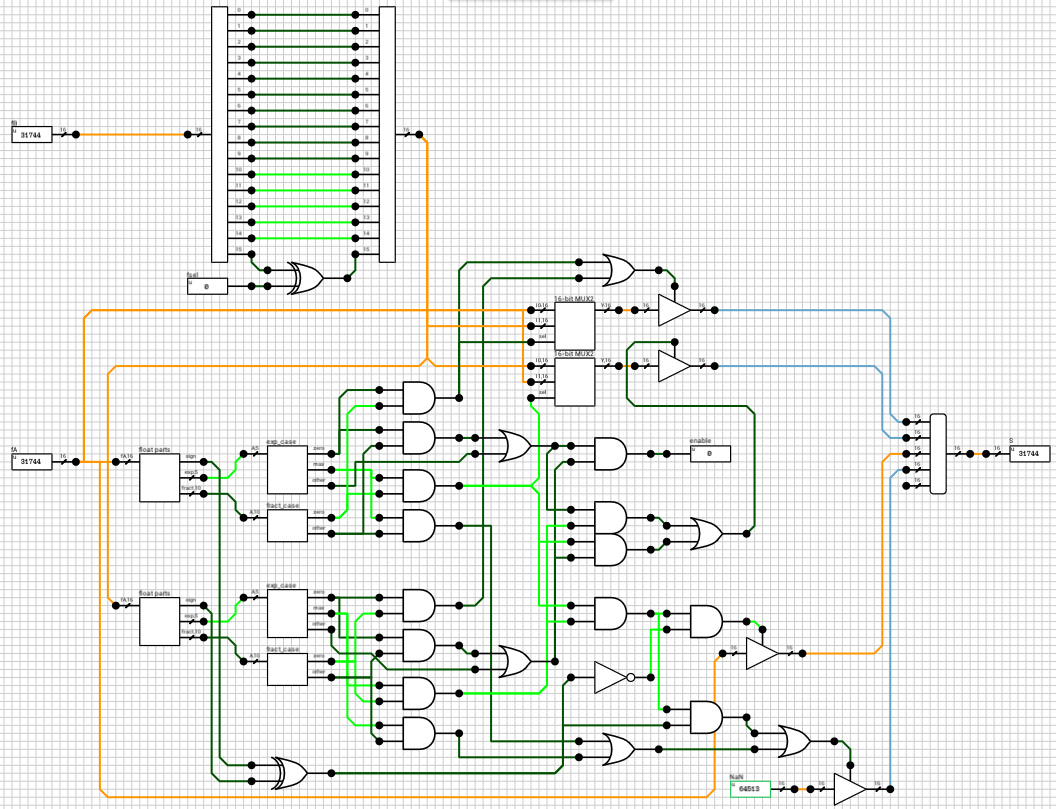
There are 2 bugs in the n_case code from the paper.

First, the classification of inputs A and B (intermediate signals outA and outB) are wrong when A or B are powers of 2 (0 < E < 255 and M = 0). Both codes on pages 22 and 96 end up producing a value of 000 for outA and outB, meaning the numbers are zero. In order to fix this problem, we just have to ignore the mantissa, in case E is in the range (0, 255) (or (0, 31) in our case of 16-bit numbers).

The second bug has to do with the treatment of B. The n_case block takes as input only the two numbers and ignores the selected operation. If fsel is 1 (subtraction), B’s sign should be reversed before checking the special cases. If we don’t do that, subtracting any number from 0 will result in the number itself, instead of its negative value (e.g. 0 - 1 = 1).

Both problems have been addressed in the circuit shown in figure 2. Other than that, the rest of the circuit consists of simple checks for each case. I decided to reverse B’s sign before making any checks, in case of subtraction. This means that 0 - 0 results in a negative zero, because the case where A is zero has higher priority than the case where B is zero. Not much of a problem, but it should be mentioned.

Step 2: Prepare for addition

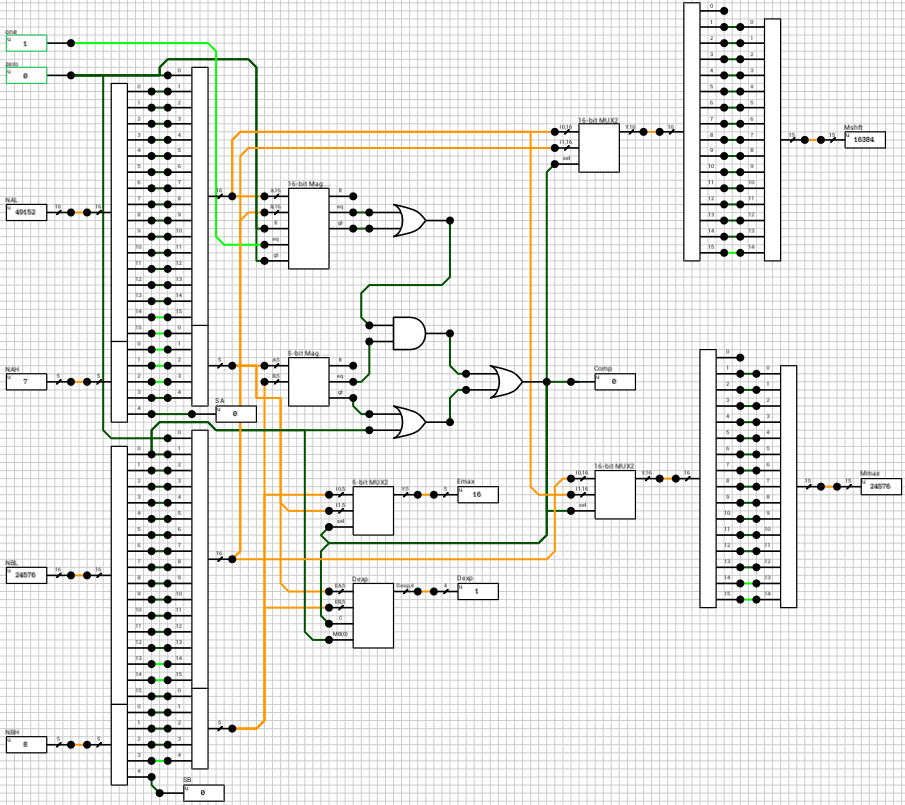
If the enable output of the n_case component is HIGH, it means that both A and B are regular numbers (normals or subnormals). Before being able to add them together, we have to align their decimal points. This is done by finding the exponent of the largest number and shifting the mantissa of the other to the right, until both exponents are equal. Remember that shifting the decimal point to the left means that the mantissa is shifted to the right. Also, for each shifted position, the exponent is incremented by 1. This part is handled by the preadder component (figure 3).

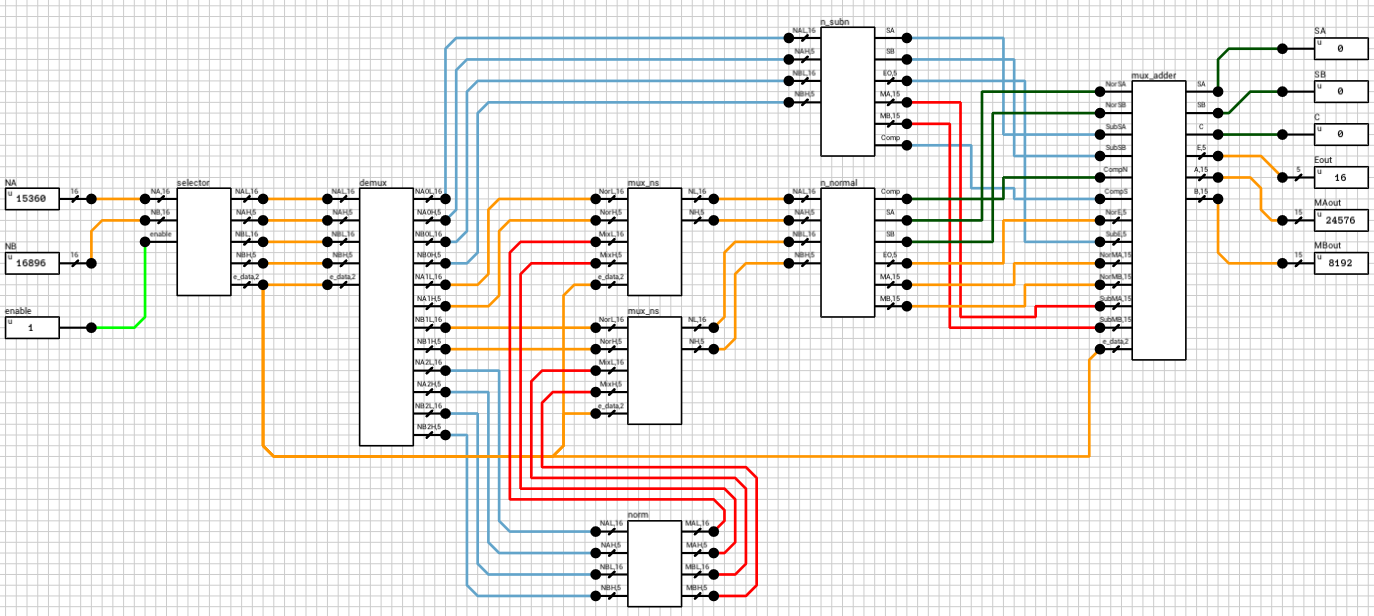
The preadder takes as input the two 16-bit numbers and the enable signal from the n_case component. First it expands both numbers to 21 bits, by introducing the implicit bit (1 for normals and 0 for subnormals) and adding 4 guard bits at the end. This is done in the selector (figure 4). The selector also outputs a 2-bit signal e_data indicating the type of both numbers (00 when both are subnormals, 01 when both are normals and 10 in case of a combination).

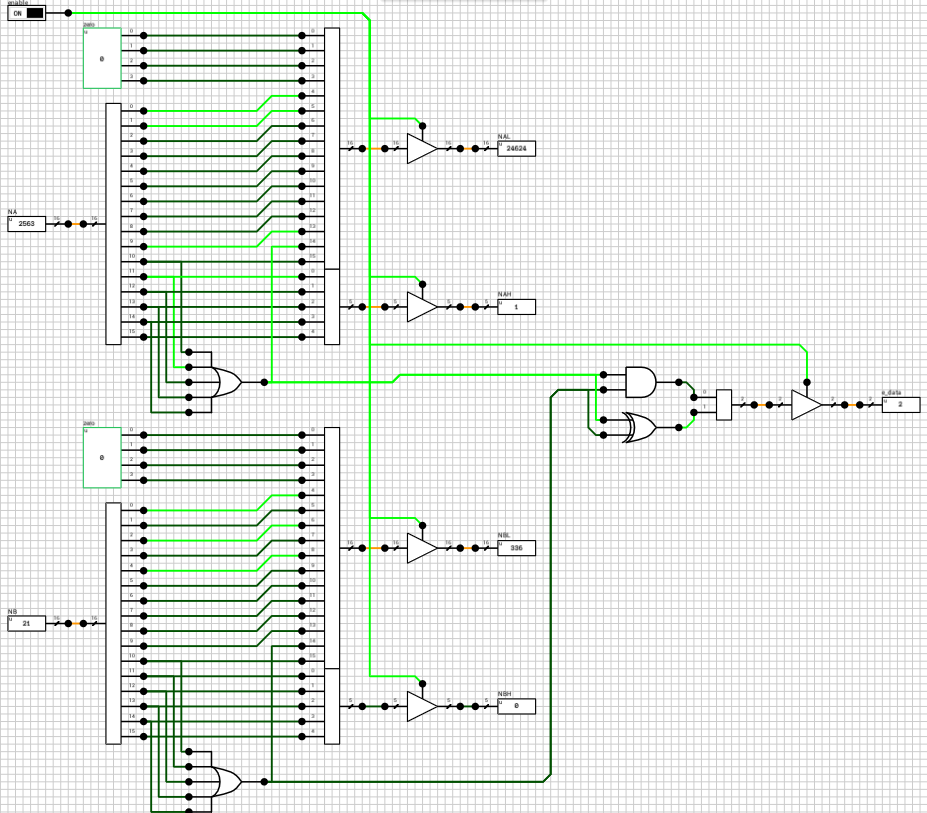
Note that the expanded 21-bit numbers are broken into 2 signals. A 16-bit for the lower part and a 5-bit signal for the higher part.

After expanding the numbers, depending on the value of e_data the correct path is chosen. If both numbers are subnormals, they are handled by the n_subn block (figure 5). In this case the output exponent is 0 (which the same for both numbers). The two mantissas are compared and the largest one is placed on MA and the other on MB. If the A input is larger than B, then Comp is HIGH, otherwise it’s LOW.

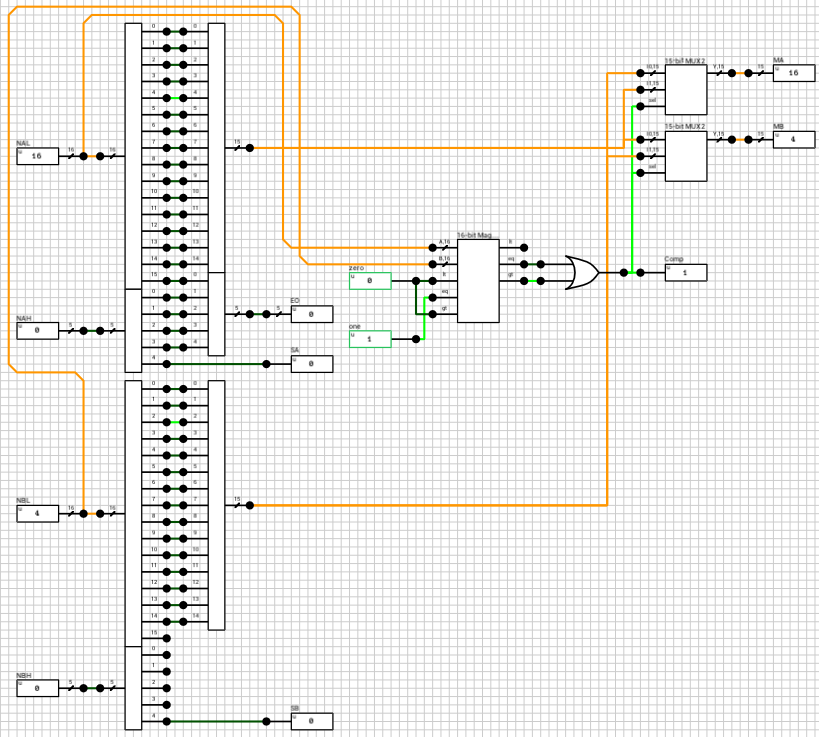
Side note: I’ve used a 16-bit magnitude comparator to compare the 2 mantissas, eventhough the extended mantissas are 15 bits wide. The 16th bit is taken from the exponent, because I know that both numbers are subnormals and thus have an exponent of zero.

If the numbers are both normals or a combination of a normal and a subnormal, they are routed to the n_normal block (figure 6 and figure 7). Again both numbers are compared and the output exponent EO is set to the largest exponent. MA holds the largest number’s mantissa. The smaller mantissa (Mshft output from the comp_exp component) is shifted to the right based on the difference of the two exponents.

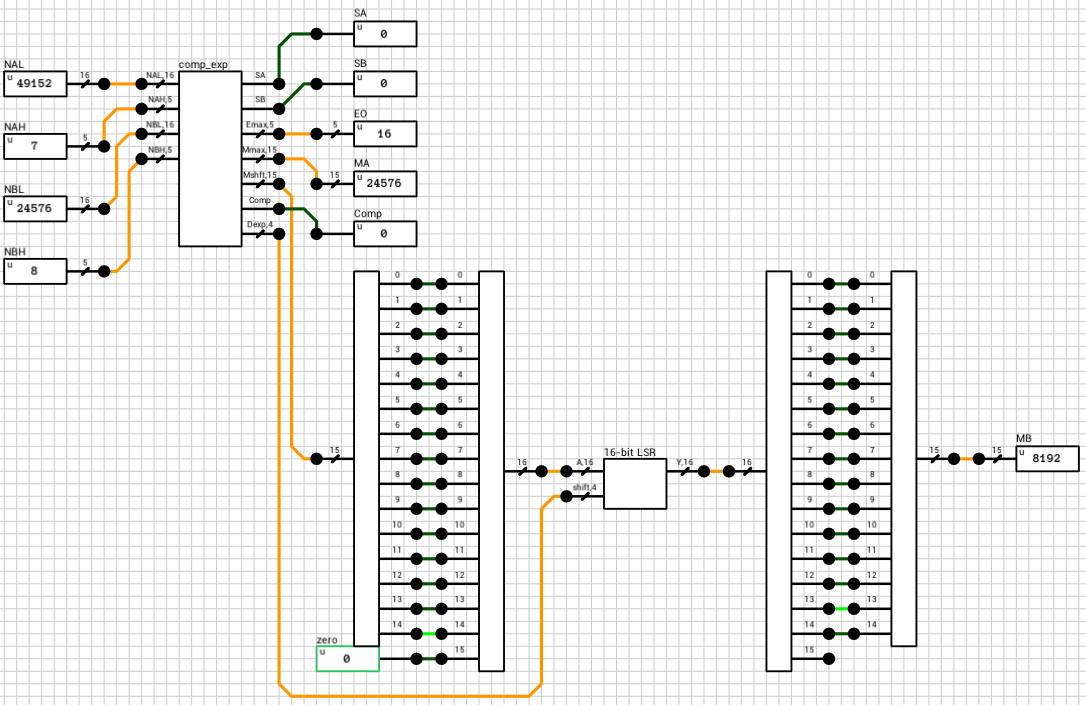
Side note: The comp_exp component uses the same 16-bit magnitude comparator as in the previous case. This time, since the exponents are non-zero, I made the 1st bit equal to 0 and the rest of the bits come from the extended mantissa.

After this step, all outputs from n_subn and n_normal are routed to the mux_adder and the final outputs of the preadder are calculated, based on e_data.

The outputs of the preadder block are the following:

• SA and SB: The signs of the two numbers
• C: 1-bit flag indicating if number A is larger than number B
• Eout: The final exponent, equal to the largest exponent
• MAout: The mantissa of the largest number
• MBout: The mantissa of the smallest number

Step 3: The addition/subtraction

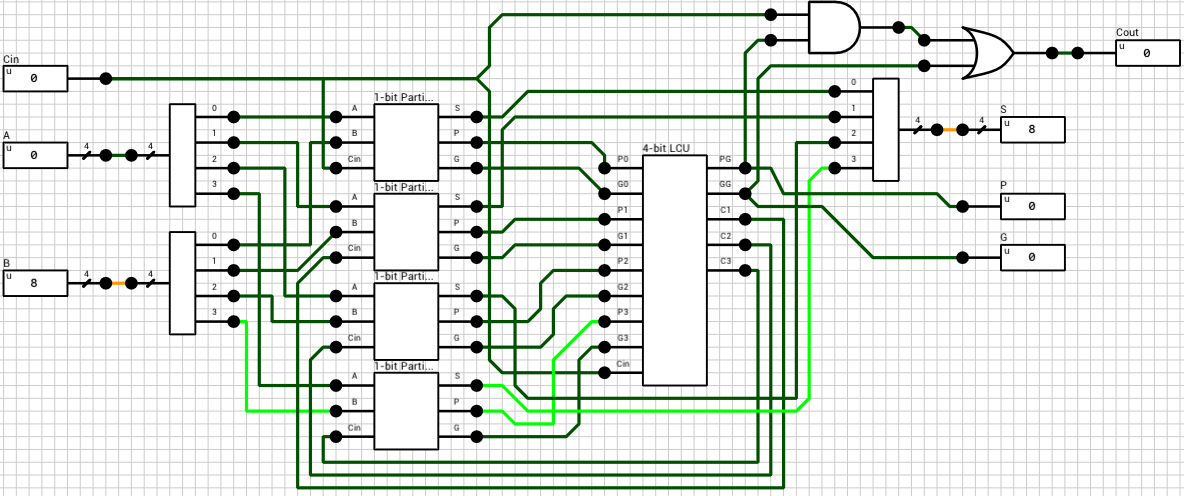
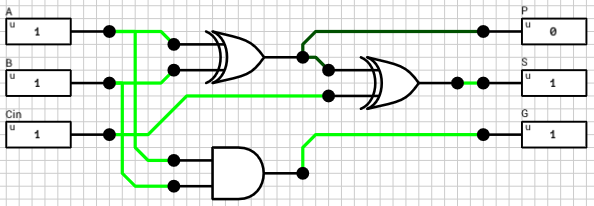
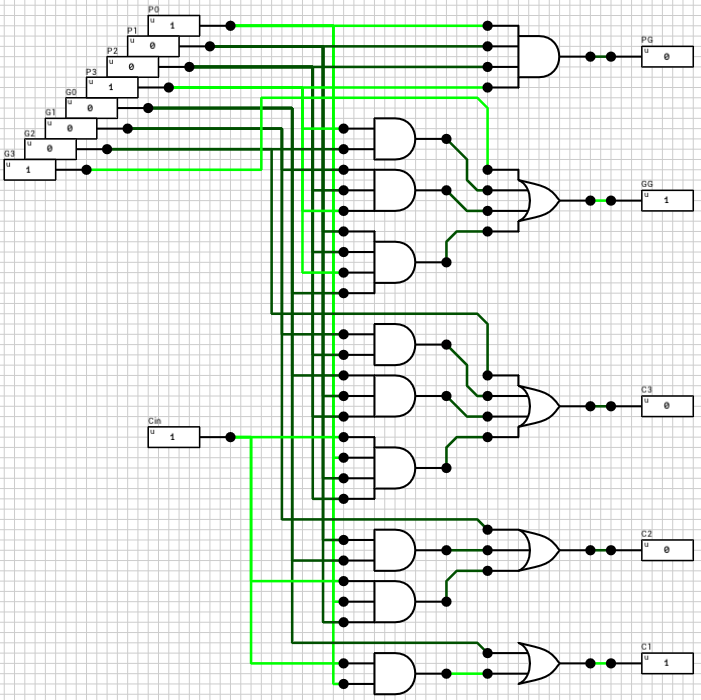
We now have both numbers in the order and the format required to perform the selected operation. Since both exponents are equal, the only thing required is to add/subtract the mantissas. This is handled by the block_adder component (figure 8). The block_adder takes as input the two signs, SA and SB, the two mantissas A and B, the selected operation (0 for addition, 1 for subtraction) and the Comp flag which indicates if A is larger than B.

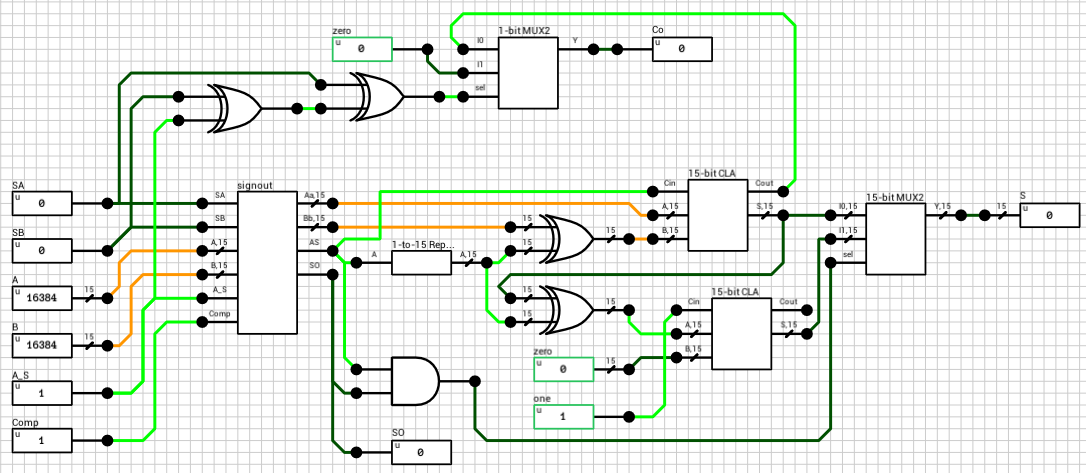
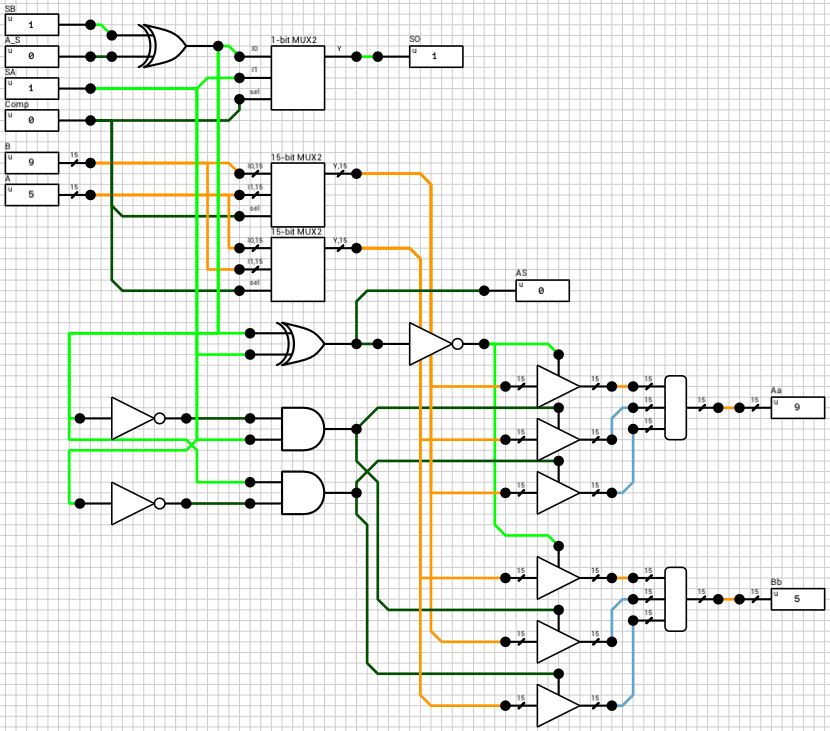
The signout block (figure 9) is responsible for calculating the sign of the result, the true operation to be performed between the two inputs and for reordering the inputs in case the true operation is different than the selected operation. The true operation is the actual operation to be performed between the two inputs. I.e. if we subtract a negative number from a positive number, the true operator is addition, which is different than the selected subtraction.

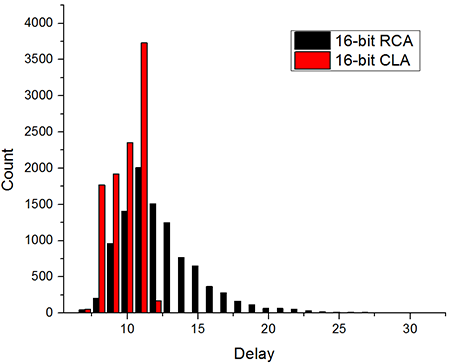
The final addition/subtraction is performed using a trimmed 16-bit CLA. The circuit is similar to the one presented in the previous article, with the only difference being that the 16-th bit of the result is used as the carry out of the addition and the sum is only 15 bits wide.

Step 4: Normalization

We now have all the parts necessary to reconstruct the result. Figure 10 shows the normalization block (norm_vector from the paper).

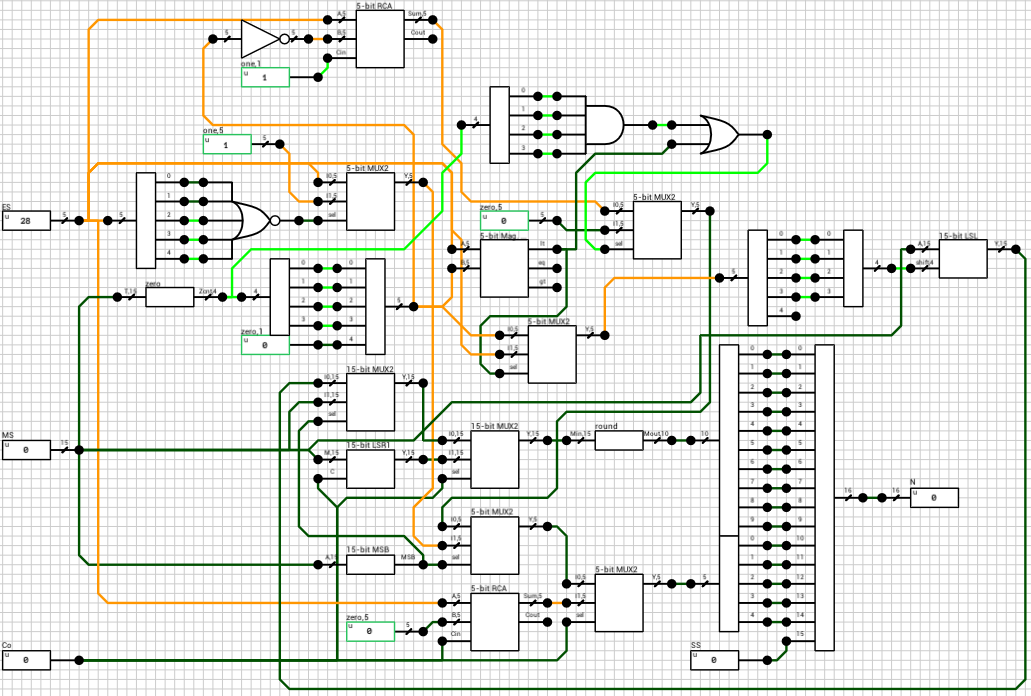
It might seem a bit more complicated than necessary so I’ll try to describe the circuit in pseudocode below. The job of this component is to normalize the mantissa and correct the exponent accordingly. It gets as inputs the sign of the result (SS), the exponent (ES), the mantissa (MS) and the carry out of the addition (Co). Note that this part is very different than the one found in the paper. I probably didn’t understand the VHDL correctly and my attempts to map it directly to circuit ended up producing invalid results. The circuit shown in figure 10 seems to behave correctly in all tested cases.

There are several cases to consider when normalizing the mantissa. The code below shows all of them in pseudocode (assume a combined 16-bit number ZX.YYYYYYYYYYYYYY, where Z = Co and X = MSB(M))

if Z == 1 then
    E' = E + 1
    M' = M >> 1 // M' = 1.XYYYYYYYYYYYYY
else
    if X == 1 then
        if E == 0 then // subnormal + subnormal = normal
            E' = 1
            M' = M // M' = 1.YYYYYYYYYYYYYY
        else
            E' = E
            M' = M // M' = 1.YYYYYYYYYYYYYY
        end
    else
        lz = leading_zeroes(M)
        if E < lz or lz == 15 then
            E' = 0
            M' = M << E // Shift the mantissa to the left until the exponent becomes zero
        else
            E' = E - lz
            M' = M << lz // Shift the mantissa to the left until an 1 appears on the MSB
        endif
    endif
endif

Hope it’s a bit more clear than the circuit :)

There are 2 special cases to consider. When adding two subnormal numbers, the result might end up being a normal (e.g. 0x0200 + 0x0200 = 0x0400 which is the smallest normal). In this case Z = Co = 0, X = MSB(M) = 1 and E = 0. The mantissa is already normalized (has an one at the MSB), so the exponent needs to be incremented to 1. If it’s left at 0, the result will be wrong when rounding the mantissa (see below).

The other case is then both X and Z are zero. In this case we have to shift the mantissa to the left until it becomes normalized or until the the exponent gets to 0. This can happen if the number of leading zeroes in the mantissa is larger than the exponent or if the mantissa is 0 (lz = 15). If the mantissa is zero at this point, it means that the result is 0 independently of the exponent (i.e 0x4000 - 0x4000 = 0 eventhough ES = 0x10).

Side note: The leading_zeroes component has been implemented using a 32k x 4-bit ROM.

Other than those 2 cases, the rest should be easily derived from any explanation on floating point addition.

The final step after calculating E' and M' is to round the mantissa. This involves ignoring the implicit bit (15-th bit) and rounding the guard bits. In order to keep things as simple as possible I decided to just cut off the guard bits, which is effectively rounding towards zero.

The final floating point adder circuit is shown in figure 11.

Thanks for reading. Comments and corrections are welcome.

Last time I presented 2 different implementations of a 4-bit adder. The Ripple Carry adder (RCA from now on) was a bit slower in terms of gate delays compared to the Carry Lookahead adder (CLA). Today I’ll try to reuse those circuits as components in order to build 2 different versions of a 16-bit adder.

Before turning the circuits into components, and in order to keep the overhead of splitting and merging fat wires using Wire Splitters and Mergers, I replaced the 4-bit single-pin inputs A and B with 4-bit 4-pin inputs. The difference is that the generated component will have 8 individual 1-bit inputs (excluding Cin) for A and B. The same is done to the S output.

Figure 1 shows the simplified 4-bit RCA circuit and figure 2 shows the simplified 4-bit CLA circuit. Also note that the Cout output of the 4-bit CLA has been removed because it won’t be used in the 16-bit circuit.

16-bit Ripple Carry Adder

Figure 3 shows the 16-bit RCA circuit. It includes 4 instances of the 4-bit RCA component, connected in series (if it’s not obvious from the image, the order is top left -> top right -> bottom left -> bottom right; just follow the carries). If we take into account that each 4-bit RCA includes 4 1-bit Full Adders, this circuit requires 32 XOR, 32 AND and 16 OR gates. The worst case delay for this circuit is 34T (calculated using the testbench method described in the previous article), including the 2T overhead of the 16-bit merger and splitter.

16-bit Carry Lookahead Adder

The 16-bit CLA is shown in figure 4. It uses 4 instances of the 4-bit CLA component from figure 2 and 1 instance of the same Carry Lookahead Unit (CLU) used in the 4-bit CLA circuit. The CLU takes the 4 (P,G) pairs generated by the 4-bit CLAs, as well as the Cin input, and calculates PG and GG. From those two the final carry output is calculated, using the same subcircuit as in the 4-bit CLAs (Cout = GG + PG*Cin).

The total gates required for this circuit is: 32XOR + 85AND2 + 67AND4 + 51AND3 + 34OR4 + 17OR3 + 18OR2. The worst case delay is 12T, including the 2T overhead of the mergers/splitters.

Comparison

From the above it’s clear that the CLA is a lot faster than the RCA, but it requires many more gates. Looking at the maximum delays when comparing the 2 circuits might not tell the whole truth though. Figure 5 shows a histogram from 10k random changes to the inputs of both circuits. The X axis is the measured circuit delay and the Y axis is the number of occurrences. The worst case delay for the RCA might be 32T but the average is a lot less. The most frequent delays is around 11T for both circuits.

That’s all for now. Thanks for reading. Comments and corrections are welcome.

The past few days, I’ve added a basic logic analyzer in DLS (not yet released; will be available on v0.10). You can add probes in the schematic and connect them to output pins, in order to observe the timing of the signals coming out of them.

Having a way to observe signals as they pass through the circuit, instead of just observing their steady state at the end of the simulation, can help you find glitches or compare the speed of 2 different versions of the same circuit.

I decided to test it out by implementing 2 different versions of a 4-bit adder. One would be a ripple-carry adder and the other would be a carry lookahead adder. Ideally, the latter should be faster than the former (i.e. the sum and output carry should be available quicker), so let’s see if this is actually true in DLS.

But first some words about DLS, in case you haven’t heard about it before.

A few words about DLS

It’s been almost 9 months since I uploaded v0.1 of DLS on itch.io. DLS is an event-driven unit-delay 4-value digital logic simulator.

• Event driven means that a component/gate is simulated only if one of its inputs change value.
• Unit-delay means that all basic gates (AND,OR,etc.) have the same propagation delay, which is assumed to be 1 (in arbitrary time units).
• 4-value logic means that signals can be in one of 4 states, 0, 1, Undefined and Error. Undefined means either that the signal can be either 0 or 1 (e.g. AND(U,1) = U, AND(U,0) = 0), or that it’s in high impendance state (e.g. when used as input to a bus). Error is produced only by tristate buffers when the control signal is Undefined.

One of the reasons I started working on it was because apparently I suck at VHDL and I wanted an easier way to play around with logic circuits. The other reason was that I like simulations of any kind, so what’s a better way to learn how digital circuits work than writing a simulator :)

Fast forward 9 months, DLS can successfully simulate semi-complex circuits, built with either basic logic gates or scripts. There are probably a lot of things wrong in those circuits, but since they seem to work, who am I to complain :)

1-bit Half Adder

Let’s start small. A 1-bit half adder is shown in figure 1. It adds 2 1-bit binary inputs (A and B) and produces 2 1-bit outputs. One for the Sum (S) and one for the Carry (C). For more info see the wikipedia article on adders.

Taking into account that both the XOR and the AND gate is assumed to have the same propagation delay, we would expect both outputs (S and C) to settle at their final value after 1T (1T = 1 gate delay). Figure 2 confirms that.

1-bit Full Adder

Half adders aren’t that useful though. In order to add 2 (e.g.) 2-bit binary numbers you have to take into account the carry out of the LSB addition when calculating the sum of the MSB. A 1-bit full adder does that. In addition to the A and B inputs, it has a 3rd 1-bit input which is the carry of the previous, less significant, stage. Figure 3 shows the circuit of a 1-bit full adder.

From the above schematic it’s obvious that the maximum time required for a stable signal at the S output is 2T, when one of A or B switches value (but not the other), which forces the first XOR gate to change value.

The maximum time for the Cout output is 3T, because the AND gate in the Carry part of the circuit (lower right) has to wait 1T until the value of the first XOR is computed. E.g. B=0, A=0->1 and Cin=0->1.

Figure 4 shows the timing graph from various changes to the inputs of the full adder.

There’s one glitch in this circuit. For A = Cin = 1 and B = 1->0, Cout changes value twice. This is because the first AND gate changes value at T=1 which forces the OR gate to switch at T=2. But at T=2 the second AND gate changes value which in turn makes the OR gate to switch again at T=3.

Is it possible to fix that glitch and keep the same latency? Probably not, but we should keep that in mind in case we want to use Cout as the clock input in a sequential circuit.

A note about critical paths

Finding the critical path of circuits like those presented above might be relatively easy to be done by hand. As circuits gets more complicated, finding the critical path is a very tedious process. To be honest I haven’t researched the subject until I started writing this article, so I can’t comment on any methods used in professional simulators.

Instead of trying to implement an existing algorithm to calculate the critical path of the circuits in this article, I used a testbench (you can write testbenches in DLS using Lua by the way :)). The testbench iterates 1000 times giving random values to all circuit inputs, and simulating the circuit once in each iteration. The current simulation time is read in every iteration, and the maximum dT is calculated. The input changes that produced the maximum dT give us the critical path of the circuit.

With that out of the way, lets move on.

4-bit Ripple Carry Adder

The easiest way to build wider adders is to connect multiple 1-bit full adders in series. After all, this is the way we add two numbers on paper, isn’t it? The carry output of the i-th adder is used as the carry in to the (i+1)-th adder. The Cout of the last adder is the carry produced by the N-bit addition. This kind of adder is called a ripple carry adder.

Figure 5 shows a 4-bit ripple carry adder, which uses 4 instances of the 1-bit full adder component shown above.

Sidenote: The circuit in fig. 5 has 2 4-bit inputs, A and B. In order to get the individual bit values from these 2 inputs we have to use a Wire splitter. In reality, there’s no such thing as a 4-bit wire, so there’s no need for such component. In DLS though, in order to be able to create manageable components (with as few I/O pins as possible), we have to use “fat” wires with splitters and mergers. Because DLS is a unit-delay simulator, those components must have a delay of at least 1T in order to work correctly. This might affect the timing of the circuit but since the same parts will be used later for the lookahead carry adder, it shouldn’t affect the comparison. The same is true for the 4-bit S output which requires a wire merger.

In figure 6 the timing for various changes to the inputs of the above circuit is shown. The maximum latency of this circuit is 10T. One of the configurations which require that amount of time to compute is show in the figure (A=13->10, B=5 and Cin=1).

4-bit Carry-Lookahead Adder

Analyzing the theory behind Carry-lookahead Adders is beyong the scope of this article. For details on them you can check the corresponding wikipedia article.

Figure 7 shows the circuit of a 4-bit Carry-lookahead adder. The 4 1-bit Full adders have been replaced by 1-bit Partial adders (figure 8) and a Lookahead Carry Unit (LCU) (figure 9) has been added. The LCU’s function is to calculate PG and GG which is used for the final carry output, as well as the carries which will be used as inputs for the last 3 partial adders.

The maximum latency of this circuit is 6T, with the critical path being from the inputs to S (Cout has been calculated 2T earlier). Figure 10 shows one of the worst cases (A=4->12, B=6->13, Cin=0->1).

Closing

Apparently Carry-lookahead adders are actually faster than Ripple-carry adders, even in DLS! The extra latency introduced by the wire splitters and mergers is present in both versions, so it shouldn’t affect the comparison.

Next time, I’ll try expanding both adders to 16 bits to see if the difference gets even larger (it should). The problem with 16 bits, in case we want to reuse both of the above circuits as components, is that it requires splitting 2 16-bit wires and merging them into 4-bit groups, which will in turn be connected to the individual 4-bit adders. This alone adds a latency of 3T + 3T (3T for splitting inputs + 3T for merging outputs), but again the comparison should be fair if we apply the same methodology to both versions (I suspect that even if we cheat a bit in favor of the ripple carry adder, the CLA will still be faster overall).

Thank you for reading. Hope to be able to write more about circuits and DLS in the following weeks/months. So if you find any mistakes or have any comments on what I wrote, I’d appreciate you feedback.